Математическая смекалка

1).Математическая смекалка

Петя и Вася (начинает Петя) по очереди стирают буквы из набора «МАТЕМАТИЧЕСКАЯ ЗАДАЧА». За один ход разрешается стереть или ровно одну букву, или все одинаковые буквы. Выигрывает тот, кто сотрет последнюю букву. Кто выиграет в этой игре и какой должна быть выигрышная стратегия?

2). Кот Леопольд

Перед котом Леопольдом пять мышиных норок, расположенных в ряд. В одной из этих норок спряталась мышка. Леопольд может засунуть лапу в любую из норок и попробовать поймать мышку. Мышка боится кота, поэтому после каждой его попытки обязательно перебегает в соседнюю норку справа или слева. Может ли кот гарантированно поймать мышку? Если да, то как он должен действовать?

3). Обналичивание

На Петином счету в банке лежит 500 долларов. Банк разрешает совершать операции только двух видов: снимать 300 долларов или добавлять 198 долларов.
Какую максимальную сумму Петя может снять со счета, если других денег у него нет?

4). Отмерить время с помощью песочных часов

При помощи только 4- и 7-минутных песочных часов точно отмерьте девять минут.

5). Максимальное расстояние на автомобиле

У вас есть автомобиль с пустым баком вместительностью 20л и есть три бочки с топливом, каждая по 100л. В автомобиле можно увезти не больше одной бочки. Как при таких условиях проехать максимальное расстояние, если на 1км расходуется 1л топлива?

6). Переправа

Командиру взвода нужно переправить через реку 10 солдат. На реке нет мостов, и ни один солдат не может переплывать реку вплавь. Тут командир увидел лодку, в которой сидели два мальчика. Лодка могла удержать либо двоих мальчиков, либо одного солдата.
Как командир переправил солдат на другой берег, используя лодку?

7). Юный математик

Три друга делят 24 яблока. Пока у них есть три кучки: 11, 7 и 6 яблок соотвественно, но они хотят поделить их поровну. Один из этих друзей, математик, предложил двум другим такое пари:
— Вы должны будете уравнять количество яблок в кучках, но строго по моей системе: из одной кучки берёте столько яблок, сколько их в той кучке, куда вы добавлять собираетесь. Но сделать это вы должны строго за 3 перекладывания. Сможете — все яблоки ваши, нет — они мои.
— Давай! — согласились двое. Подумали с минутку и сумели так сделать. А как они смогли так сделать?

8). Переправа, переправа

Семья (папа, мама, сын и бабушка) ночью подошла к мосту, способному выдержать только двух человек одновременно. По мосту можно двигаться только с фонариком. Известно, что папа может перейти мост в одну сторону за минуту, мама — за две, сын — за пять и бабушка — за десять минут. Фонарик у них один. Светить издали нельзя. Носить друг друга на руках тоже. Если по мосту идут двое, время перехода определяется наиболее медлительным членом семьи. Как семье переправиться за 17 минут?

9). Монеты и кошельки

У вас есть 1000 монет и десять пустых кошельков. Вам нужно распределить все монеты между кошельками таким образом, чтобы по запросу вы могли выдать любое число монет от 1 до 1000. Причем выдавать монеты можно только вместе с кошельками, перекладывать монеты между кошельками нельзя. Как это сделать?

10). Что быстрее

Что быстрее: проехать весь путь на велосипеде или половину пути проехать на мотоцикле, а вторую половину пройти пешком, если скорость мотоцикла в два раза больше скорости велосипеда, а скорость велосипеда в свою очередь, в два раза больше скорости пешехода?

11). Вычисление скидок

В магазине одежды дважды последовательно уценили свитер — на 30% и на 10%. Сколько составила бы эквивалентная разовая скидка?

12). Пчелы

Задача из древнего индийского трактата:
— если 1/5 пчелиного роя полетела на цветы лаванды, 1/3 – на цветы липы, утроенная разность этих чисел полетела на дерево, а одна пчела продолжала летать между ароматными кетаки и малати, то сколько всего было пчел?

13). Задача на сообразительность

Что должно стоять вместо знака вопроса:

14). Попpыгyнья стpекоза

Попpыгyнья стрекоза половину времени каждых сyток кpасного лета спала, тpетью часть вpемени каждых сyток танцевала, шестyю часть — пела. Остальное вpемя она pешила посвятить подготовке к зиме. Сколько часов в сyтки стpекоза готовилась к зиме?

15). 12 девяток

В ряд записано 12 девяток: 9 9 9 9 9 9 9 9 9 9 9 9.
Поставьте между ними знаки действий (+, -, :, х) так, чтобы получилось 2000.

16). Задача для репетитора

В рассказе А. П. Чехова «Репетитор» гимназист Егор Зиберов не сумел решить арифметическую задачу, а отец репетируемого ученика, отставной губернский секретарь Удодов, пощелкав на счетах, получил правильный ответ. Решите и Вы эту задачу арифметически. Интересно, умеют ли решать подобные задачи современные репетиторы. Вот она.
Купец купил 138 аршин черного и синего сукна за 540 руб. Спрашивается, сколько аршин купил он и того и другого, если синее стоило 5 руб. за аршин, а черное — 3 руб.?

17). 10 точек

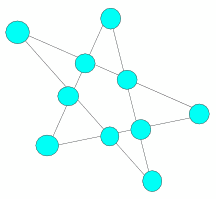
Соедините 10 точек пятью линиями так, чтобы на каждой линии лежало ровно 4 точки.

18). Ряды и точки

Расположите 12 точек в 7 рядов по 4 точки в каждом.

19). 8 кусочков

Разделите приведенную фигуру на 8 одинаковых частей:

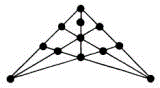
20). Печать царя Соломона

Сколько равносторонних треугольников изображено на знаменитой печати царя Соломона, изображенной на его гробнице.

21). Чайная комбинаторика

В магазине «Все для чая» есть 5 разных чашек и 3 разных блюдца. Сколькими способами можно купить чашку с блюдцем?

22). Дни недели

Сегодня не воскресенье, а завтра не среда. Вчера была не пятница, а позавчера был не понедельник. Завтра не воскресенье, и вчера было не воскресенье. Послезавтра не суббота и не воскресенье. Вчера был не понедельник, и не среда. Позавчера была не среда, а завтра не вторник. Да, и сегодня не среда. Какой же сегодня день недели, если учесть, что одно утверждение в списке — ложно?

23). Определите профессию

В отделении Сбербанка работают: кассир, контролер и заведующий. Их фамилии: Борисов, Иванов и Сидоров. Кассир не имеет ни братьев, ни сестер и меньше всех ростом. Сидоров женат на сестре Борисова и ростом выше контролера.
Назовите фамилии кассира, контролера и заведующего.

24). Семья

В семье пять человек: муж, жена, их сын, сестра мужа и отец жены. Их профессии — инженер, юрист, слесарь, учитель и экономист. Известно, что юрист и учитель — не кровные родственники. Слесарь младше экономиста, и оба играют в футбол за сборную своего завода. Инженер моложе учителя, но старше жены своего брата. Назовите профессии каждого.

25). Мудрецы развлекаются

Решили как-то пять мудрецов поразвлечься. Взяли они десять колпаков, причем разноцветных — шесть красных, два белых и два синих, позвали независимую персону, он каждому должен надеть на голову по колпаку. Естественно, все это происходит в кромешной тьме и никто из мудрецов даже не знает, какие колпаки оказались лишними. Затем они выходят на свет, смотрят друг на друга, и кто первый определит, какой на нем колпак, тот и победит. Кто станет победителем, если на трех участниках красные колпаки, на одном — синий и на одном — белый?

26). Правильно расставить знаки

В выражении 8 8 8 8 8 расставьте знаки «+», «-«, «/» и «* » и/или скобки так, чтобы получилось:c
а) 1; б) 2; в) 3; г) 4; д) 5.

27). Храмы и монеты

Паломник во время визита в далекую страну посетил 9 храмов. Чтобы попасть в каждый из храмов, необходимо подняться по лестнице из 100 ступеней. Паломник при подъеме по лестнице жертвует в пользу храма по одной монете на каждой ступеньке. В самом храме он жертвует половину от имеющихся у него монет. И на обратном пути при спуске паломник также жертвует по одной монете на каждой ступеньке.
После посещения всех 9 храмов паломник обнаружил, что пожертвовал все свои монеты. Сколько монет было у него изначально?