Какая рекламная кампания провалилась из-за математической неграмотности американцев?
В начале 1980-х годов сеть ресторанов быстрого питания A&W запустила масштабную рекламную кампанию своего гамбургера. В отличие от похожего сэндвича в 1/4 фунта из Макдоналдс, гамбургер A&W весил 1/3 фунта и стоил чуть дешевле, а покупатели говорили, что он вкуснее. Несмотря на всё это, кампания провалилась. Позже A&W провела исследование и выявила причину: многие клиенты не понимали истинного значения дробных чисел. Предложение казалось им невыгодным, так как 3 меньше 4.
Что происходит с параллельными прямыми в геометрии Лобачевского?
По распространённому мнению, в геометрии Лобачевского параллельные прямые пересекаются. На самом деле, они не могут пересекаться ни в какой геометрии в силу самого определения параллельности. Главным же отличием геометрии Лобачевского от евклидовой является то, что через точку, не лежащую на данной прямой, можно провести не одну, а по крайней мере две не пересекающих её прямых, находящихся в той же плоскости.
Почему возникла десятичная система счисления?
Используемая нами десятичная система счисления возникла по причине того, что у человека на руках 10 пальцев. Способность к абстрактному счёту появилась у людей не сразу, а использовать для счёта именно пальцы оказалось удобнее всего. Цивилизация майя и независимо от них чукчи исторически использовали двадцатичную систему счисления, применяя пальцы не только рук, но и ног. В основе распространённых в древних Шумере и Вавилоне двенадцатеричной и шестидесятиричной систем тоже было использование рук: большим пальцем отсчитывались фаланги других пальцев ладони, число которых равно 12.
Кто стал профессором математики, не имея математического образования после средней школы?
Стивен Хокинг — один из крупнейших физиков-теоретиков и популяризатор науки. В рассказе о себе Хокинг упомянул, что стал профессором математики, не получая никакого математического образования со времён средней школы. Когда Хокинг начал преподавать математику в Оксфорде, он читал учебник, опережая собственных студентов на две недели.
Кто решил сложную математическую проблему, приняв её за домашнее задание?
Американский математик Джордж Данциг, будучи аспирантом университета, однажды опоздал на урок и принял написанные на доске уравнения за домашнее задание. Оно показалось ему сложнее обычного, но через несколько дней он смог его выполнить. Оказалось, что он решил две «нерешаемые» проблемы в статистике, над которыми бились многие учёные.
Какие оценки по математике получал Эйнштейн в школе?
Во многих источниках, зачастую с целью ободрения плохо успевающих учеников, встречается утверждение, что Эйнштейн завалил в школе математику или, более того, вообще учился из рук вон плохо по всем предметам. На самом деле всё обстояло не так: Альберт ещё в раннем возрасте начал проявлять талант в математике и знал её далеко за пределами школьной программы. Позднее Эйнштейн не смог поступить в Швейцарскую высшую политехническую школу Цюриха, показав высшие результаты по физике и математике, но не добрав нужное количество баллов в других дисциплинах. Подтянув эти предметы, он через год в возрасте 17 лет стал студентом данного заведения.
Чем пожертвовала Софья Ковалевская ради возможности заниматься наукой?
Чтобы получить возможность заниматься наукой, Софье Ковалевской пришлось заключить фиктивный брак и уехать из России. В то время российские университеты просто не принимали женщин, а чтобы эмигрировать, девушка должна была иметь согласие отца или мужа. Так как отец Софьи был категорически против, она вышла замуж за молодого учёного Владимира Ковалевского. Хотя в итоге их брак стал фактическим, и у них родилась дочь.
Как связаны между собой шахматы, рис и разорение?
Известна притча о том, как один человек предлагает другому расплатиться с ним за некоторую услугу следующим образом: на первую клетку шахматной доски тот положит одно рисовое зёрнышко, на вторую — два и так далее: на каждую следующую клетку вдвое больше, чем на предыдущую. В результате тот, кто расплачивается таким образом, непременно разоряется. Это неудивительно: подсчитано, что общий вес риса составит более 460 миллиардов тонн.
Какому правилу, выведенному Леонардо, подчиняются ствол и ветви деревьев?
Леонардо да Винчи вывел правило, согласно которому квадрат диаметра ствола дерева равен сумме квадратов диаметров ветвей, взятых на общей фиксированной высоте. Более поздние исследования подтвердили его с одним лишь отличием — степень в формуле необязательно равняется 2, а лежит в пределах от 1,8 до 2,3. Традиционно считалось, что эта закономерность объясняется тем, что у дерева с такой структурой оптимальный механизм снабжения веток питательными веществами. Однако в 2010 году американский физик Кристоф Эллой нашёл более простое механическое объяснение феномену: если рассматривать дерево как фрактал, то закон Леонардо минимизирует вероятность слома веток под воздействием ветра.
Какой последовательностью описывается расположение листьев на ветках растений?
Листья на ветке растения всегда располагаются в строгом порядке, отстоя друг от друга на определённый угол по или против часовой стрелки. Величина угла разная у различных растений, но её всегда можно описать дробью, в числителе и знаменателе которой — числа из ряда Фибоначчи. Например, у бука этот угол равен 1/3, или 120°, у дуба и абрикоса — 2/5, у груши и тополя — 3/8, у ивы и миндаля — 5/13 и т.д. Такое расположение позволяет листьям наиболее эффективно получать влагу и солнечный свет.
Какие овощи имеют соцветия в виде фракталов?
Соцветия капусты сорта романеско представляют собой фракталы. Бутоны растения описываются логарифмической спиралью и состоят из более мелких бутонов, тоже закрученных подобным образом. Эта самоподобная структура повторяется несколько раз.
Фракта́л (лат fractus — дроблёный, сломанный, разбитый) — математическое множество, обладающее свойством самоподобия (объект, в точности или приближённо совпадающий с частью себя самого, то есть целое имеет ту же форму, что и одна или более частей).
Первая женщина – математик
Первой женщиной-математиком в истории, считается гречанка Гипатия, жившая в египетской Александрии в IV-V веках нашей эры.
Самый древний математический труд
Самый древний математический труд был найден в Свазиленде – кость бабуина с выбитыми чёрточками (кость из Лембобо), которые предположительно были результатом какого-то вычисления. Возраст кости – 37 тысяч лет. Во Франции был найден ещё более сложный математический труд – волчья кость, на которой выбиты чёрточки, сгруппированные по пять штук. Возраст кости – около 30 тысяч лет.
Ну и наконец знаменитая кость из Ишанго (Конго) на которой выбиты группы простых чисел. Считается, что кость возникла 18-20 тысяч лет назад.
А вот древнейшим математическим текстом могут считаться вавилонские таблички с кодовым названием Plimpton 322, созданные в 1800-1900 году до нашей эры.
Судьба отрицательных чисел
Мы считаем отрицательные числа чем-то естественным, но так было далеко не всегда.
Впервые отрицательные числа были узаконены в Китае в III веке, но использовались лишь для исключительных случаев, так как считались, в общем, бесмыссленными. Чуть позднее отрицательные числа стали использоваться в Индии для обозначения долгов, но западнее они не прижились – знаменитый Диофант Александрийский утверждал, что уравнение 4x+20=0 – абсурдно.
В Европе отрицательные числа появились благодаря Леонардо Пизанскому (Фибоначчи), который тоже ввёл его для решения финансовых задач с долгами – в 1202 году он впервые использовал отрицательные числа для подсчёта своих убытков.
Тем не менее до XVII века отрицательные числа были “в загоне” и даже в XVII веке знаменитый математик Блез Паскаль утверждал, что 0-4=0 ибо нет такого числа, которое может быть меньше ничего, а вплоть до XIX века математики часто отбрасывали в своих вычислениях отрицательные числа, считая их бесмыссленными…
Египетское умножение
У древних египтян не было таблиц умножения и правил. Тем не менее, умножать они умели и пользовались для этого “компьютерным” способом – разложением чисел в двоичный ряд.
Как же они это делали? А вот как:
Например, нужно умножить 22 на 35.
Записываем 22 35
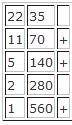Теперь делим левое число на 2, а правое умножаем на 2.
Итак,
А теперь складываем 70+140+560=770
Правильный результат!
Египетское деление
Процесс египетского деления был очень сложный и сопряженный с несколькими попытками.
Например, делим 153 на 9.
Для этого умножаем 9 столько раз на 2 пока 9 не превысит 153.
То есть:
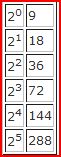Теперь замечаем, что 153=9+144, первое соответствует 20, второе 24. Стало быть результат 20+24=17.
Древнеегипетские дроби
Египтяне не знали дробей вроде 2/3 или 3/4. Никаких числителей! Египетские жрецы оперировали лишь с дробями, где числитель был всегда 1 и дробь записывалась так: целое число с овалом над ним. То есть 4 с овалом означало 1/4.
А что же дроби вроде 5/6 ? Египетские математики раскладывали их на дроби с числителем 1. То есть 1/2 + 1/3. То есть 2 и 3 с овалом вверху.
Ну что ж, это просто. 2/7 = 1/7 + 1/7. Отнюдь! Ещё одним правилом египтян было отсутствие в ряду дробей повторяющихся чисел. То есть 2/7 по их мнению было 1/4+1/28.
В общем, непроста была жизнь египетского математика…
Интересные факты о числе Пи
В математике есть множество постоянных величин. Самая известная из них это число Пи.
Представляем Вам интересные факты о числе Пи. Пи — неизменная и самая распространенная константа в математических вычислениях.
Символ, который обозначает Пи, существует более 250 лет. Впервые он появился в 1706 году благодаря Уильяму Джонсу (1746-1794г.)
В 2002 году был зафиксирован новый мировой рекорд вычисления Пи. Ученый из Японии смог на компьютере произвести вычисления 1240000 млн цифр числа Пи.
Знаменитая компания Givenchy выпустила коллекцию духов под названием Pi.
Интересно и то, что число Пи используют и при вычислении прогноза погоды.
А если Пи записать в виде дроби, то оно не будет иметь конца, а так же повторений.
Занимательно, что пирамида Хеопса является неким воплощением числа Пи в природе? Так, соотношение между высотой и периметром основания дает в результате число 3,14.
Существуют даже люди, которые отважились ставить рекорды на запоминания символов Пи. На сегодня это 83 тыс символов после запятой. Именно такой рекорд смог поставить выходец из Японии Акира Харагучи.
Когда празднуют день числа Пи?
У числа Пи есть два неофициальных праздника. Первый — 14 марта, потому что этот день в Америке записывается как 3.14. Второй — 22 июля, которое в европейском формате записывается 22/7, а значение такой дроби является достаточно популярным приближённым значением числа Пи.
Памятник числу Пи в Сиэтле на ступенях перед зданием Музея искусств
Перельман и гипотеза Пуанкаре
Григорию Перельману удалось доказать знаменитую гипотезу Пуанкаре. О сути открытия практически не сообщалось, зато все знали о том, что автор отказался от вознаграждения в 1 000 000 $.
Теория Анри Пуанкаре была выдвинута в 1904 году. До этого парижский профессор занимался самыми разными областями науки, в том числе и теорией относительности. Но прославился своей гипотезой в области топологии.
Топология– наука о свойствах геометрических фигур, которые не изменяются при деформациях, происходящих без разрывов. К примеру, воздушный шарик можно с легкостью деформировать в самые разные фигуры – это делают для детей в цирке. Но потребуется разрезать шарик, чтобы скрутить из него бублик (в геометрии — тор) – другого способа не существует. Или наоборот: возьмите резиновый бублик и попробуйте «превратить» его в шар. Не получится! По своим топологическим свойствам поверхности сферы и тора несовместимы.
Если насчет двумерных поверхностей сферы и тора все было решено еще в XIX веке, для более многомерных случаев потребовалось гораздо больше времени. В этом, собственно, и состоит суть гипотезы Пуанкаре, которая расширяет закономерность и на трёхмерные случаи. Вот вкратце суть гипотез: пространство является трёхмерной сферой с точностью до деформации. Если говорить ещё проще, то любой объект без сквозных отверстий и дыр может быть преобразован в сферу, если он находится в системе координат x,y,z и t(время). Значит как бы ни был деформирован объект в итоге он может стать только сферой и более ничем. Некоторые высказывают также социальную суть гипотезы, а именно: как бы человек не был сдавлен жизненными обстоятельствами, как бы это его не испортило, он всегда может вернуться к исходной точке и вернуть себе своё доброе имя.
Доказательство гипотезы из области высшей математики. Интересно, что сам Перельман отчего-то не потрудился довести свое решение до окончательного блеска. Описав решение «в целом» ещё в 2002 году, он в марте 2003 года провел серию лекций в ряде университетов Америки и Европы. И, если раньше многие ученые пытались доказать гипотезу и всякий раз в их доказательствах находились «белые пятна», то на этот раз ни один из рецензентов не смог обнаружить в предложенном Перельманом варианте ошибок. Даже если вопросы и возникали, то профессор с лёгкостью объяснял все этапы своего доказательства. Однако публикации в научных изданиях о своей работе математик не выпустил , а это было одним из основных условий получения премии, выдвинутым институтом Клэя (Масачусетс). До завершения работу Г. Перельмана довели китайские и американские математики, которые и выдают за окончательный вариант доказательства свои разработки.
Лист Мёбиуса
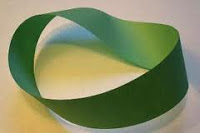Лист Мёбиуса относится к числу «математических неожиданностей». Говорят, что открыть свой «лист» ученому Мёбиусу помогла служанка, сшившая однажды неправильно концы ленты. Как бы то ни было, но в 1858 году профессор Лейпцигского университета А. Ф. Мёбиус (1790-1868) послал в Парижскую академию наук работу, включавшую сведения об этом листе. Несколько лет он дожидался рассмотрения своей работы и, не дождавшись, опубликовал ее результаты. Одновременно с Мёбиусом изобрел этот лист и И. Б.Листинг (1808-1882), профессор Геттингенского университета. Что же поразило этих двух немецких профессоров?
У листа Мёбиуса всего одна сторона! Мы привыкли к тому, что у всякой поверхности, с которой мы имеем дело— две стороны. Давайте убедимся в этом: начните постепенно окрашивать лист в какой-нибудь цвет, начиная с любого места, и по завершении работы, вы обнаружите, что весь он полностью окрашен. Вторая неожиданность поджидает нас в тот момент, когда мы попробуем разрезать лист Мёбиуса по его средней линии. «Нормальное» кольцо при этом бы распалось на два куска, а лист Мёбиуса при этом превратится в одно перекрученное кольцо.
Свойства таких геометрических объектов изучает математическая наука — топология. Но главная ценность листа Мёбиуса состоит в том, что он дал толчок новым обширным математическим исследованиям. Именно поэтому его часто считают символом современной математики и изображают на различных эмблемах и значках.
Памятник ленте Мёбиуса в Минске
Треугольник Паскаля
Треугольник Паскаля — бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван в честь Блеза Паскаля. Числа, составляющие треугольник Паскаля, возникают естественным образом в алгебре, комбинаторике, теории вероятностей, математическом анализе, теории чисел.
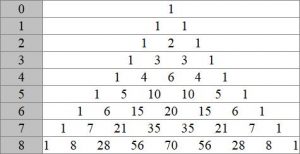
Первое упоминание треугольной последовательности биномиальных коэффициентов под названием meru-prastaara встречается в комментарии индийского математика X века Халаюдхи к трудам другого математика, Пингалы. Треугольник исследуется также Омаром Хайямом около 1100 года, поэтому в Иране эту схему называют треугольником Хайяма. В 1303 году была выпущена книга «Яшмовое зеркало четырёх элементов» китайского математика Чжу Шицзе, в которой был изображен треугольник Паскаля на одной из иллюстраций; считается, что изобрёл его другой китайский математик, Ян Хуэй (поэтому китайцы называют его треугольником Яна Хуэя). На титульном листе учебника арифметики, написанном в 1529 году Петром Апианом, астрономом из Ингольштадтского университета, также изображён треугольник Паскаля. А в 1653 году (в других источниках в 1655 году или в 1665 году) вышла книга Блеза Паскаля «Трактат об арифметическом треугольнике».
Свойства:
- Числа треугольника симметричны (равны) относительно вертикальной оси.
- В строке с номером n:
- первое и последнее числа равны 1.
- второе и предпоследнее числа равны n.
- третье число равно сумме номеров предшествующих строк.
- четвёртое число является тетраэдрическим.
- Сумма чисел восходящей диагонали, начинающейся с первого элемента (n-1)-й строки, есть n-е число Фибоначчи:
- Сумма чисел n-й строки треугольника Паскаля равна 2n.
- Все числа в n-й строке, кроме единиц, делятся на число n, если и только если n является простым числом.
- Если в строке с нечётным номером сложить все числа с порядковыми номерами вида 3n, 3n+1, 3n+2, то первые две суммы будут равны, а третья на 1 меньше.
- Каждое число в треугольнике равно количеству способов добраться до него из вершины, перемещаясь либо вправо-вниз, либо влево-вниз.
Цитаты
Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок. В то же время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего. Столь необычные свойства позволяют считать треугольник Паскаля одной из наиболее изящных схем во всей математике.
(Мартин Гарднер)
Логарифмическая спираль
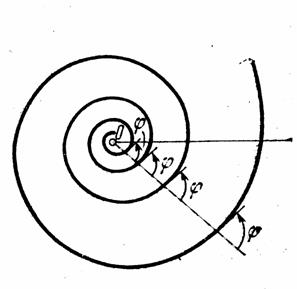Логарифмическая спираль была впервые описана Декартом и позже интенсивно исследована Бернулли, который называл её Spira mirabilis — «удивительная спираль». Декарт искал кривую, обладающую свойством, подобным свойству окружности, так чтобы касательная в каждой точке образовывала с радиус-вектором в каждой точке один и тот же угол. Он показал, что это условие равносильно тому, что полярные углы для точек кривой пропорциональны логарифмам радиус-векторов.
 |
 |
 |
 |
Якоб Бернулли хотел, чтобы на его могиле была выгравирована логарифмическая спираль, но вместо этого по ошибке на его надгробие поместили архимедову спираль. Тем не менее, надпись на латыни, выгравированная согласно завещанию вокруг спирали, «EADEM MUTATA RESURGO» («изменённая, я вновь воскресаю»), свидетельствует о том, что имеется в виду именно логарифмическая спираль, которая обладает замечательным свойством восстанавливать свою форму после различных преобразований.
Надгробие Бернулли.
