Задание 1.1
Задача 1. По кругу расставлены цифры 1, 2, 3, 4, 5, 6, 7, 8, 9 в произвольном порядке. Каждые три цифры, стоящие подряд по часовой стрелке, образуют трехзначное число. Зависит ли сумма всех девяти таких трехзначных чисел от порядка, в котором расставлены цифры? Найдите их сумму.
Для решения задачи достаточно заметить, что каждая цифра один раз участвует в разряде единиц, один раз — в разряде десятков и один раз — в разряде сотен. Поскольку сумма данных в условии задачи цифр равна 45, получаем требуемую сумму 45 + 450 + 4500 = 4995,
которая не зависит от расстановки цифр.
Задача 2. Два пирата играли на золотые монеты. Сначала первый проиграл половину своих монет и отдал второму. Потом второй проиграл половину своих монет, потом снова первый проиграл половину своих. В результате у первого оказалось 19 монет, а у второго 43. Сколько монет было у каждого пирата до начала игры?
Решая эту задачу следует рассуждать с конца. Схема игры показана в таблице:
| Шаг в игре | Первый пират | Второй пират |
| Конец игры | 19 | 43 |
| 3 | 19 | 43 |
| 2 | 38 | 24 |
| 1 | 14 | 48 |
| Начало игры | 28 | 34 |
Задача 3. Из горячего крана ванна наполняется за 23 минуты, из холодного — за 17 минут. Катя открыла горячий кран. Через сколько минут она должна открыть холодный, чтобы горячей воды к моменту наполнения ванны налилось в 1,5 раза больше, чем холодной?
Примем объем всей ванны за 1. Тогда для того, чтобы горячей воды в ванне оказалось в 1,5 раза больше, чем холодной, она должна занять 3/5 объема ванны. Так как за 1 минуту горячей водой заполняется 1/23 объема ванны, то кран с горячей водой должен быть открыт
3/5 : 1/23 = 69/5 (мин.).
Холодная вода к моменту наполнения ванны должна занимать 1 — 3/5 = 2/5 ее объема. Так как за 1 минуту кран с холодной водой заполняет 1/17 объема ванны, он должен быть открыт
2/5 : 1/17 = 34/5 (мин.).
Следовательно, если сначала открыть кран с горячей водой, то кран с холодной водой следует открыть через
69/5 — 34/5 = 7 (мин.).
Задача 4.«Бабушка, сколько лет твоему внуку?» — «Моему внуку столько месяцев, сколько мне лет, а вместе нам 65 лет». Сколько лет внуку?
Из условия задачи ясно, что бабушка в 12 раз старше своего внука. Обозначая возраст внука — х лет, бабушки — 12 х лет, получаем:
х + 12х = 65,
откуда х = 5. Поэтому внуку 5 лет.
Задача 5.. На диагонали ВD квадрата АВСD взяты точки Е и Н так, что прямая АЕ пересекает сторону ВС в точке М, а прямая АН пересекает сторону СD в точке К и СМ = СК. Найдите длины диагоналей квадрата, если ВЕ = 3, ЕН = 4.
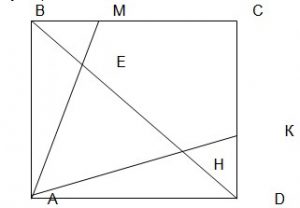
Из условия следует равенство треугольников АВМ и АDК (см. рисунок).
Поэтому ∠ВАЕ = ∠DАН. Кроме того, АВ = АD и ∠АВЕ = ∠АDН. Поэтому треугольники АВЕ и АDН равны, и, значит DН = ВЕ = 3. Тогда АС = ВD = 10.
Задание 1.2
Задача 1.Расшифровать равенство
КЛОП + КЛОП + КЛОП + КЛОП = ПОЛК.
(одинаковыми буквами обозначены одинаковые цифры, разными — разные).
Во-первых, следует отметить, что число ПОЛК — четное. Значит, цифра К — четная, отлична от 0 и не превосходит 2. Поэтому К = 2, а следовательно, П равно 8 или 9, но поскольку именно произведение чисел 4 и 8 оканчивается цифрой 2, то П = 8. Теперь ясно, что
ПОЛК < 9000,
а, следовательно, КЛОП < 2250. Поэтому Л — это 1 или 0. Если Л = 0, то число ПОЛК на 4 не делится, значит, Л = 1. Теперь нетрудно определить, что букве О соответствует цифра 7. Получаем:
2178 + 2178 + 2178 + 2178 = 8712.
Задача 2.В некотором году три месяца подряд содержат всего по четыре воскресенья. Докажите, что один из этих месяцев — февраль.
Из условия следует, что указанные три месяца содержат 12 воскресений. Известно, что воскресенье — седьмой день недели, Значит, эти три месяца насчитываю меньше, чем 13 •7 = 91 день. Остается заметить, что любые три подряд идущих месяца, среди которых нет февраля, насчитывают не меньше чем 91 день.
Задача 3.Из пункта А в пункт В выехал велосипедист. Одновременно из В в А по той же дороге выехал мотоциклист. Через 30 минут велосипедисту оставалось проехать 3 км до середины пути; мотоциклист же через 20 минут после начала движения уже отъехал от середины пути 2 км. Через какое время после начала движения произошла встреча велосипедиста с мотоциклистом?
Пусть S — расстояние АВ в километрах. Тогда за время 30 минут велосипедист проехал (S/2 — 3) км, и поэтому его скорость равна
(S/2 — 3) / (1/2) = 2(S/2 — 3) = (S — 6) км/ч.
Мотоциклист за 20 минут проехал
(S/2 + 2) / (1/3) = 3(S/2 + 2) = (3 S/2 + 6) км/ч.
Скорость сближения велосипедиста с мотоциклистом равнялась, таким образом,
S — 6 + 3 S/2 + 6 = 5 S/2 (км/ч),
а встреча произошла через
S : (5 S/2) = 2/5 (ч),
то есть через 24 минуты после начала движения.
Задача 4.Высоты остроугольного треугольника АВС пересекаются в точке Н. Известно, что АВ = СН. Найдите величину угла АСВ.
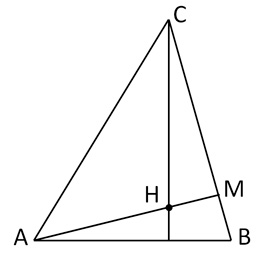
Опустим из вершины А высоту АМ на сторону ВС (см. рисунок).
Углы НСВ и МАВ равны как острые углы с взаимно перпендикулярными сторонами (возможно и другое обоснование:
∠НСВ = 90о — ∠В и ∠МАВ = 90о — ∠В).
Следовательно, прямоугольные треугольники СНМ и АВМ равны по гипотенузе и острому углу. Поэтому, СМ = АМ, а, следовательно, треугольник АМС — равнобедренный и прямоугольный. Получаем: ∠АСВ = 45о.
Задача 5.На доске записаны числа 14 и 19. К уже записанным на доске числам разрешается дописать число, равное сумме любых двух из уже записанных. Можно ли, повторяя эту операцию, получить на доске число 1998?
Число 1998 можно представить в виде
1998 = 19 • 2 + 1960 = 19 • 2 + 14 • 140.
Поэтому операции, которые приведут к появлению на доске числа 1998 могут быть следующими,.
14, 19, 14 + 19 = 33, 33+ 19 =52, 52 + 14 = 66,.
66 + 14 = 80, 80 + 14 = 94, …, 1984 + 14 = 1998..
Задание 1.3
Задача 1.Известно, что cos a + cos ß = a и sin a + sin ß = b, a2 + b2 ≠ 0. Выразите cos (a — ß) через a и b.
Возведем в квадрат данные равенства:
(cos a + cos ß)2 = cos2 a + 2 cos a cos ß + cos2 ß = a2,
(sin a + sin ß)2 = sin2 a + 2 sin a sin ß + sin2 ß = b2.
Складывая полученные равенства, получаем:
cos2 a + 2 cos a cos ß + cos2 ß + sin2 a + 2 sin a sin ß
+ sin2 ß = 2 + 2 (cos a cos ß + sin a sin ß) =
= 2 + 2 cos (a — ß) = a2 + b2.
Выражая из последнего равенства cos (a — ß) получаем:
cos (a — ß) = (a2 + b2 — 2) / 2.
Задача 2.На рисунке изображены графики трех квадратных трехчленов.
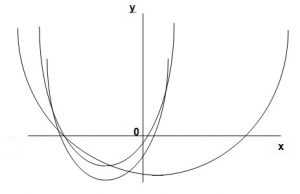
Могут ли это быть трехчлены ax2 + bx + c, cx2 + ax + b и bx2+ cx + a?
Значения данных трехчленов при х = 1 равны
a + b + c. Поэтому, если бы приведенные на рисунке параболы были бы графиками данных трехчленов, то они пересекались бы в точке с абсциссой 1, и общее число точек пересечения у них было бы не 6, как это видно на рисунке, а не превосходило бы 4.
Задача 3.
Сумма цифр натурального числа А равна сумме цифр числа 3А. Докажите, что:
1. А делится на 3;
2. А делится на 9;
3. Верно ли, что А обязательно делится на 27?
Для доказательства утверждений 1 и 2 следует воспользоваться признаками делимости на 3 и на 9. Контрпримерами для пункта 3 являются числа, например, А = 9, А = 18.
Задача 4.
Петя, Вася, Коля и Миша играли в футбол. Кто-то из них разбил мячом стекло. На вопрос «Кто это сделал?» пять свидетелей ответили так:
1. То ли Петя, то ли Вася.
2. То ли Петя, то ли Коля,
3. То ли Коля, то ли Миша.
4. То ли Миша, то ли Вася.
5. Не знаю.
Потом оказалось, что трое свидетелей сказали правду, а двое — неправду. Знал ли пятый свидетель, кто разбил окно?
Нетрудно заметить, что на каждого из мальчиков, как на возможного виновника указали ровно двое из первых четырех свидетелей. Поэтому, кто бы ни разбил стекло, двое из первых четырех свидетелей сказали правду, а двое — неправду. Но по условию правду сказали трое. По-этому третьим сказавшим правду свидетелем может быть только пятый свидетель. А это означает, что он не знал, кто разбил стекло.
Задача 5.
Дан параллелограмм АВСD. На сторо-нах ВС и СD и диагонали ВD взяты соответственно точки Н, К, М так, что МН || АВ, МК || АD. Отрезки АН и АК пересекают диагональ ВD в точках Е и Т соответственно. Доказать, что площадь треугольника АЕТ равна сумме площадей треугольников ВЕН и ТКD.
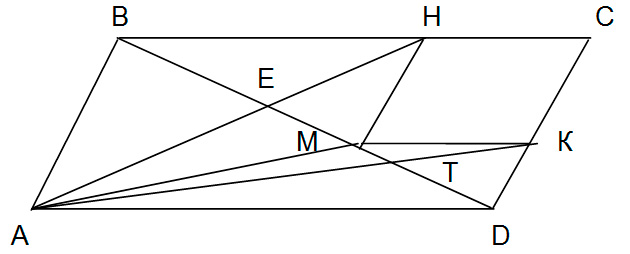
Из условия задачи следует, что АМКD — трапеция (см. рисунок).
Поэтому площади треугольников АМТ и DТК равны, по-скольку вместе с треугольником АТD они образуют равно-великие треугольники АМD и АКD. Аналогично доказываем равенство площадей треугольников АЕМ и ВЕН. Таким образом,
S АЕТ = S АМТ + S АЕМ = S DТК + S ВЕН,
что и требовалось доказать.
Задание 1.4
Задача 1. Найдите три последние цифры суммы
1! + 2! + 3! + … + 1998!
Простыми рассуждениями нетрудно убедиться, что 15! и все последующие слагаемые данной суммы в разложении на простые множители содержат не менее трех 5 и не менее трех 2, а поэтому каждое заканчивается как минимум тремя нулями. Поскольку три последние цифры произведения и суммы зависят только от трех последних цифр сомножителей и слагаемых, то при решении задачи следует обращать внимание только на эти три цифры. В следующей таблице приведены три последние цифры первых четырнадцати слагаемых:
| 1! | 2! | 3! | 4! | 5! | 6! | 7! | 8! | 9! | 10! | 11! | 12! | 13! | 14! |
| 1 | 2 | 6 | 24 | 120 | 720 | 720 | 040 | 320 | 880 | 800 | 600 | 800 | 200 |
Теперь нетрудно определить, что три последние цифры данной суммы 313
Задача 2.
Найдите все натуральные числа n, при которых уравнение
х2 — 7nх + 150 = 0
имеет два целых корня.
Предположим, что уравнение имеет два целых корня. Тогда по формулам теоремы Виета имеем равенства:
a b = 150, a + b = 7n.
Поскольку n натуральное, то a b и a + b — положительные, а, следовательно, оба корня уравнения положительны. Полагая для определенности a ≥ b, получаем несколько возможностей:
1. a = 150, b = 1;
2. a = 75, b = 2;
3. a = 50, b = 3;
4. a = 30, b = 5;
5. a = 25, b = 6;
6. a = 15, b = 10.
Простым перебором убеждаемся, что только в случаях 2 и 4 сумма a + b делится на 7. Следовательно, a + b = 77, или a + b = 35. В первом случае n = 11, во втором n = 5.
Обратно, в случае, когда n = 11 уравнение имеет два целых корня 30 и 5, и, если n = 5, уравнение имеет два целых корня 75 и 2.
Задача 3.
Решить уравнение
2х + sin4 х = 2 + sin4 1
Рассмотрим функцию f(х) = 2х + sin4 х. Уравнение принимает вид:
f(х) = f(1).
Убедимся, что рассматриваемая функция возрастающая. Имеем:
f′(х) = 2+ 4 sin3 x cos x = 2 + 2 sin2 x sin 2x =
= 2 + (1 — cos 2x) sin 2x = 2 + sin 2x — 0.5 sin 4x.
Учитывая область изменения функции sin a, можем оценить производную функцию и убедиться, что f′(х) > 0. Значит, рассматриваемая функция возрастающая.
Поэтому данное уравнение имеет единственный корень
х = 1.
Задача 4.
Четырехугольник АВСD вписан в окружность. Известны длины его сторон:
АВ = 32, ВС = 5, СD = 45, АD = 60.
Найдите угол между прямыми АВ и СD.
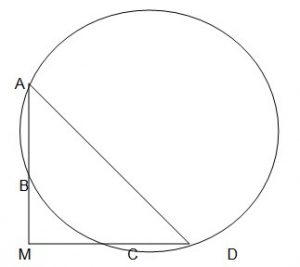
Продолжим стороны АВ и СD данного четырехугольника до пересечения их в точке М. Так как четырехугольник вписан в окружность, то ∠АDС + ∠АВС = 180°,
и, следовательно, ∠АDС = ∠МВС (по свойству смежных углов). Аналогично доказываем, что ∠DАВ = ∠ВСМ. Поэтому треугольники МВС и МDА подобны по двум углам, а, следовательно,
МD : ВМ = АМ : МС = АD : ВС.
Из полученных соотношений получаем:
ВМ = 4, МС = 3.
Имеем:
ВМ2 + МС2 = 16 + 9 = 25 =ВС2.
По теореме, обратной теореме Пифагора, делаем вывод, что треугольник ВСМ прямоугольный. Значит, искомый угол ВМС — прямой.
Задача 5.
На доске записано уравнение
х4+ …х3 + …х2 + …х + … = 0,
и двое учеников ставят вместо многоточий целые числа. Начинающий игрок стремится к тому, чтобы после четвертого шага получилось уравнение, не имеющее целых корней, второй игрок стремится к противоположному. Кто выиграет при правильной стратегии?
Вполне ясно, что на третьем шаге игры вместо трех многоточий стоят некоторые числа a, b, c. Если второй игрок поставит на последнее свободное место число
— a — b — c — 1,
то сумма коэффициентов получается равной 0. В этом случае, как легко убедиться, число 1 будет корнем уравнения. Поэтому хорошо знающий теорию ученик, всегда выигрывает.